Yusuf Sila: October 2011

YOUR POST TITLE HERE
SOME DESCRIPTION OF YOUR POST HERE

The International Mathematics Competition Problems

2:03 AM

Muhammad Yusuf , Posted in Math Competitions , 0 Comments

The list of the problems form IMC

1997	2003
1998	2004
1999	2005
2000	2006
2001	2007
2002	2010

»» READMORE...

Arithmetic Sequences and Linear Functions

1:39 AM

Muhammad Yusuf , Posted in Algebra , 1 Comment

Problem: Consider the diagrams below. If the pattern continues, how many squares will there be in Diagram 50? Diagram 100?

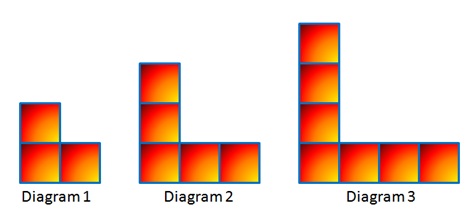
Figure 1 - A sequence of L-shaped square blocks.

In solving problems, it is important to present data in which we can easily see patterns. Table 1 shows the relationship between the diagram numbers and thenumber of squares.

Table 1 – The relationship between the diagram number and the number of squares.

We can solve this problem by “brute force” extending the table up to Figure 100, but that is not very “mathematical.” What mathematics had taught us is to find patterns, and, if possible, make generalizations. Using the first term, theconstant difference and the diagram number, we can form a numerical expression that when simplified will result to the number of squares as shown in Table 2. Looking at the table, we can say that the first term is 3, and thedifference is 2. Using this pattern, it is now easy to compute the number ofsquares in any diagram number.

Examine the table and see if you can find the pattern before proceeding.

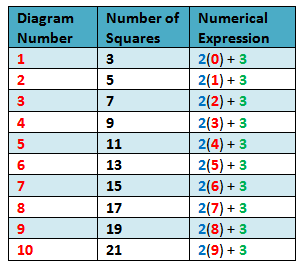
Table 2 - Numerical expressions describing the number of squares in each diagram number.

In Table 2, we can see that in the numerical expression column, the constantdifference 2 and the first term 3 appear in every term. The changing quantity (variable) is the figure number - 1. Using the pattern, it is easy to see that the 50^th term is 2(50-1) + 3 = 101 and the 100^th term is 2(100-1) + 3 = 201. In general, Figure n will have 2(n-1) + 3 = 2n + 1 squares.

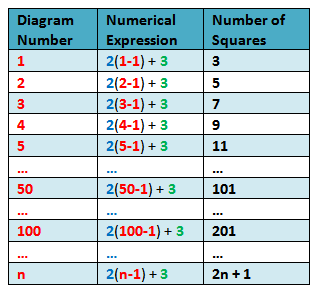
Table 3 – Generalized expression describing the number ofsquares.

Let us denote the nth term of a sequence by t_n. Since 2 and 3 are constants, if we let a be the first term of the sequence and d be the constant difference, then the formula that will describe the nth term of the sequence is

t_n = a(n-1) + d

Arithmetic Sequence as a Linear Function

Figure 2 shows the graph of the arithmetic sequence and its trend line denoted by the dashed line. Since we have a constant difference, we have a linear function. If we want to get the equation of the linear function that describes the relationship in our problem, since several ordered pairs are given, we can use the slope intercept formula.

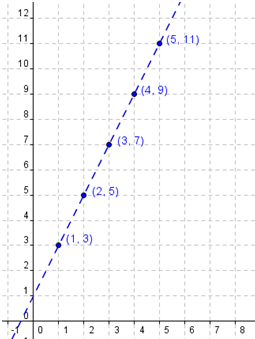
Figure 2 – Graph of the d(n) = 2n + 1, where d(n) is the diagram number

If we extend the trend line, it will pass the (0,1) (Why?). Getting (1,3) as our second point, the slope m will be (3-1)/(1-0) = 2. Hence, the equation of our line will be y = 2x + 1 which is of the same form as t_n = 2n + 1 in Table 3.

»» READMORE...

The Algebraic and Geometric Proofs of Pythagorean Theorem

1:37 AM

Muhammad Yusuf , Posted in Geometry , 0 Comments

The Pythagorean theorem states that if a right triangle has side lengths $a, b$ and $c$ , and that $c$ is its hypotenuse (longest side), then the sum of the squares of the two shorter side lengths is equal to the square of the length of its hypotenuse.

Figure 1 – A right triangle with side lengths a, b and c.

Putting it in equation form, following the abovementioned conditions, the following relationship holds:

$a^2 + b^2 = c^2$ .

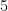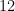For example, if a right triangle has side lengths $5$ and $12$ , then the length of its hypotenuse is 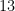$13$ , since $c^2 = 5^2 + 12^2 \Rightarrow c = 13$ .

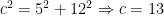Exercise 1: What is the hypotenuse of the triangle with sides 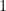$1$ and $\sqrt{3}$ ?

The converse of the theorem is also true. If the side lengths of the triangle satisfy the equation 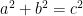$a^2 + b^2 = c^2$ , then the triangle is right. For instance, a triangle with side lengths 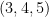$(3, 4, 5)$ satisfies the equation 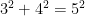$3^2 + 4^2 = 5^2$ , therefore, the said triangle is right.

Geometrically speaking, the Pythagorean theorem states that if you have a right triangle with sides $a, b$ and $c$ ( $c$ being the hypotenuse), and you constructed three squares containing the sides of the triangle as shown in Figure 2, the area of the two smaller squares when added equals the area of the largest square (click here to see animation).

Figure 2 – The geometric interpretation of the Pythagorean theoremstates that the area of the green square plus the area of the red square is equal to the area of the blue square.

One specific case is shown in Figure 3: the areas of the two smaller squares are 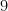$9$ and $16$ square units, and the area of the largest square is $25$ square units.

Exercise 2: Verify that the area of the largest square in Figure 3 is 25 square units.

Figure 3 – A right triangle with side lengths 3, 4 and 5.

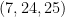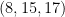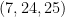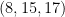Similarly, triangles with side lengths $(7, 24, 25)$ and $(8, 15, 17)$ are right triangles. If the side lengths of a right triangle are all integers, we call themPythagorean triple. Hence, $(7, 24, 25)$ and $(8, 15, 17)$ are Pythagorean triples.

Exercise 3: Give other examples of Pythagorean triples.

Exercise 4: Prove that there are infinitely many Pythagorean triples.

Proofs of the Pythagorean Theorem

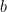There are more than 300 proofs of the Pythagorean theorem. More than 70 proofs shown in Cut-The-Knot website. Shown below are two of the proofs. Note that in proving the Pythagorean theorem, we want to show that for any right triangle with hypotenuse $c$ , and sides $a$ , and $b$ , the following relationship holds: $a^2 + b^2 = c^2$ .

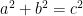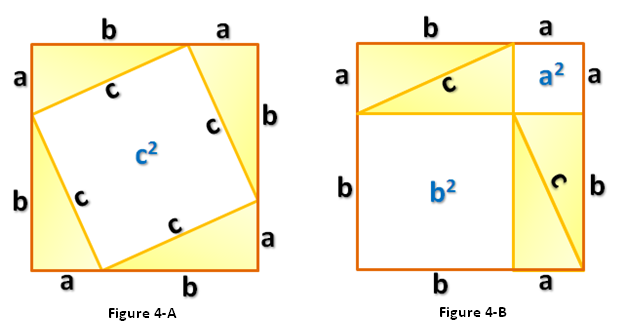
Geometric Proof

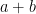First, we draw a triangle with side lengths $a, b$ and $c$ as shown in Figure 1. Next, create 4 triangles identical to it and using the triangles form a square with side lengths $a + b$ as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is $c^2$ .

Figure 4 - The Geometric proof of the Pythagorean theorem.

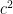Rearranging the triangles, we can also form another square with the same side length as shown in Figure 4-B.This means that the area of the white square in the Figure 4-A is equal to the sum of the areas of the white squares in Figure 4-B (Why?). That is, 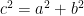$c^2 = a^2 + b^2$ which is exactly what we want to show. 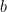*And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary $a$ and $b$ as side lengths of a right triangle), this implies that the equation 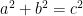$a^2 + b^2 = c^2$ stated above is always true.

Exercise 5: Prove that the quadrilateral with side length C in Figure 4-A is a square.

Algebraic Proof

In the second proof, we will now look at the yellow triangles instead of the squares. Consider Figure 4-A. We can compute the area of a square with side lengths $a + b$ using two methods: (1) we can square the side lengths and (2) we can add the area of the 4 congruent triangles and then add them to the area of the white square which is $c^2$ . If we let $A$ be the area of the square with side $b + a$ , then calculating we have

Method 1: $A = (b + a)^2 = b^2 + 2ab +a^2$

Method 2: $A = 4(1/2ab) + c^2 = 2ab + c^2$

Methods 1 and 2 calculated the area of the same square, therefore they must be equal. This means that we can equate both expressions. Equating we have,

$b^2 + 2ab + a^2 = 2ab + c^2 \Rightarrow a^2 + b^2 = c^2$