Carl Friederich Gauss is one of the most prolific mathematicians of all time. In fact,  he is considered by many as the “Prince of Mathematicians” because of his numerous contributions in different fields of mathematics.

Gauss displayed his genius at an early age. According to anecdotes, when he was in primary school, he was punished by his teacher due to misbehavior.  He was told to add the numbers from 1 to 100. He was able to compute its sum, which is 5050, in a matter of seconds.

Now, how on earth did he do it?

Well, let’s have a few examples. Since it is very hard to add 100 numbers at once, we start with smaller numbers and see if we can see a pattern.

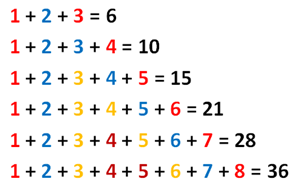
First, we observe that when the largest number is even, we can pair the numbers with the same color, that is, the last term and the first, the second term and the second to the last term, the third term and the third to the last term and so on, without a term left unpaired. In adding numbers from 1 through 6, for instance, it is clear that we have 6/2or 3 pairs.

Second, we observe that if we add the terms mentioned above, the sum of each pair is always equal to the same number. For example, in adding a number from 1 through 6, we have (1 + 6), (2 + 5) and (3 + 4), which all equals to 6 + 1, and we know that 6 is the largest number.

From above, we have 3 pairs of numbers, each of which has a sum of 7. Therefore, the sum of the numbers from 1 through 6 maybe expressed as (6/2)(6+1) = 3(7) = 21. Now try a few examples and see if our the pattern holds.

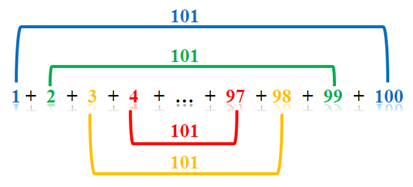
If we use this pattern, we can easily add the number from 1 through 100. We have the following pairs: (1 + 100), (2 +99), (3 + 98) and so on (see figure below).   That is, we have 100/2 pairs of numbers, each of which, has a sum of(100 + 1). Therefore, we have (100/2)(100+1) = 50(101) = 5050. This was the strategy used by the young Gauss.

Now, let us generalize the pattern. What if we add the number from 1 through any number n? That is, what is the sum of

Well, if we add the first term and the second term, we have (1 + n), (2 + (n-1)), (3 + (n-2)), and so on.

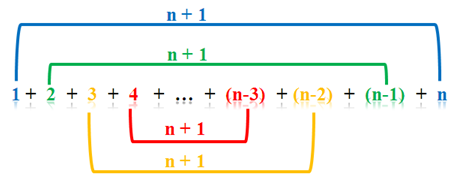
Notice that each pair has a sum of n + 1, and we have n/2 pairs of them. Therefore, the sum of all the integers from  through , or the first  positive integers is equal to

.

Exercise: Notice that the example was specified the first positive integers whose largest term is even. Explain why or why not the generalization will work if the largest integer is odd.

Another strategy

Another strategy is to let  be the sum of the first  integers and then adding another  whose order of the sum expression is reversed.

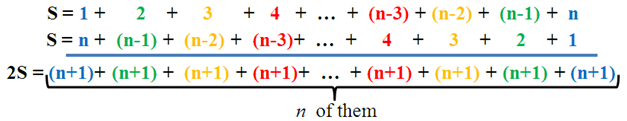
From the equation above, . Therefore, . This is similar to our answer above.

Now our conjecture is that the sum of the first n positive integers is equal to .