Arithmetic Sequences and Linear Functions
Problem: Consider the diagrams below. If the pattern continues, how many squares will there be in Diagram 50? Diagram 100?
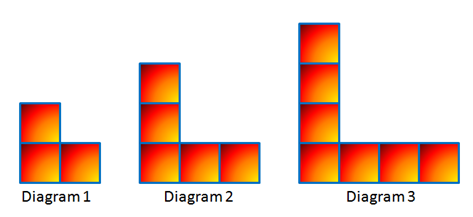
Figure 1 - A sequence of L-shaped square blocks.
In solving problems, it is important to present data in which we can easily see patterns. Table 1 shows the relationship between the diagram numbers and thenumber of squares.

Table 1 – The relationship between the diagram number and the number of squares.
We can solve this problem by “brute force” extending the table up to Figure 100, but that is not very “mathematical.” What mathematics had taught us is to find patterns, and, if possible, make generalizations. Using the first term, theconstant difference and the diagram number, we can form a numerical expression that when simplified will result to the number of squares as shown in Table 2. Looking at the table, we can say that the first term is 3, and thedifference is 2. Using this pattern, it is now easy to compute the number ofsquares in any diagram number.
Examine the table and see if you can find the pattern before proceeding.
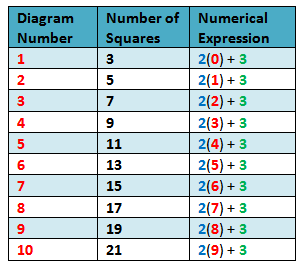
Table 2 - Numerical expressions describing the number of squares in each diagram number.
In Table 2, we can see that in the numerical expression column, the constantdifference 2 and the first term 3 appear in every term. The changing quantity (variable) is the figure number - 1. Using the pattern, it is easy to see that the 50th term is 2(50-1) + 3 = 101 and the 100th term is 2(100-1) + 3 = 201. In general, Figure n will have 2(n-1) + 3 = 2n + 1 squares.
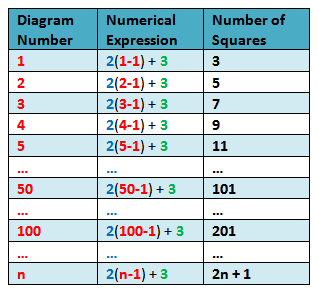
Table 3 – Generalized expression describing the number ofsquares.
Let us denote the nth term of a sequence by tn. Since 2 and 3 are constants, if we let a be the first term of the sequence and d be the constant difference, then the formula that will describe the nth term of the sequence is
tn = a(n-1) + d
Arithmetic Sequence as a Linear Function
Figure 2 shows the graph of the arithmetic sequence and its trend line denoted by the dashed line. Since we have a constant difference, we have a linear function. If we want to get the equation of the linear function that describes the relationship in our problem, since several ordered pairs are given, we can use the slope intercept formula.
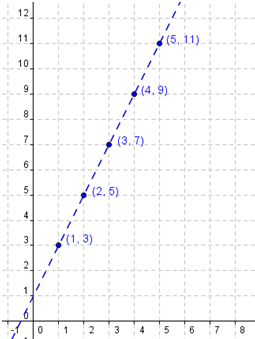
Figure 2 – Graph of the d(n) = 2n + 1, where d(n) is the diagram number
If we extend the trend line, it will pass the (0,1) (Why?). Getting (1,3) as our second point, the slope m will be (3-1)/(1-0) = 2. Hence, the equation of our line will be y = 2x + 1 which is of the same form as tn = 2n + 1 in Table 3.
The Algebraic and Geometric Proofs of Pythagorean Theorem
The Pythagorean theorem states that if a right triangle has side lengths  and
and  , and that
, and that  is its hypotenuse (longest side), then the sum of the squares of the two shorter side lengths is equal to the square of the length of its hypotenuse.
is its hypotenuse (longest side), then the sum of the squares of the two shorter side lengths is equal to the square of the length of its hypotenuse.
Putting it in equation form, following the abovementioned conditions, the following relationship holds:
For example, if a right triangle has side lengths 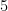 and
and 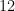 , then the length of its hypotenuse is
, then the length of its hypotenuse is 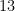 , since
, since 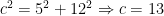 .
.
Exercise 1: What is the hypotenuse of the triangle with sides 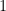 and
and  ?
?
The converse of the theorem is also true. If the side lengths of the triangle satisfy the equation 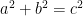 , then the triangle is right. For instance, a triangle with side lengths
, then the triangle is right. For instance, a triangle with side lengths 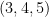 satisfies the equation
satisfies the equation 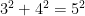 , therefore, the said triangle is right.
, therefore, the said triangle is right.
Geometrically speaking, the Pythagorean theorem states that if you have a right triangle with sides  and
and  (
( being the hypotenuse), and you constructed three squares containing the sides of the triangle as shown in Figure 2, the area of the two smaller squares when added equals the area of the largest square (click here to see animation).
being the hypotenuse), and you constructed three squares containing the sides of the triangle as shown in Figure 2, the area of the two smaller squares when added equals the area of the largest square (click here to see animation).

Figure 2 – The geometric interpretation of the Pythagorean theoremstates that the area of the green square plus the area of the red square is equal to the area of the blue square.
One specific case is shown in Figure 3: the areas of the two smaller squares are 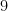 and
and  square units, and the area of the largest square is
square units, and the area of the largest square is  square units.
square units.
Exercise 2: Verify that the area of the largest square in Figure 3 is 25 square units.
Similarly, triangles with side lengths 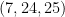 and
and 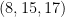 are right triangles. If the side lengths of a right triangle are all integers, we call themPythagorean triple. Hence,
are right triangles. If the side lengths of a right triangle are all integers, we call themPythagorean triple. Hence, 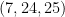 and
and 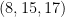 are Pythagorean triples.
are Pythagorean triples.
Exercise 3: Give other examples of Pythagorean triples.
Exercise 4: Prove that there are infinitely many Pythagorean triples.
Proofs of the Pythagorean Theorem
There are more than 300 proofs of the Pythagorean theorem. More than 70 proofs shown in Cut-The-Knot website. Shown below are two of the proofs. Note that in proving the Pythagorean theorem, we want to show that for any right triangle with hypotenuse  , and sides
, and sides  , and
, and  , the following relationship holds:
, the following relationship holds: 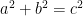 .
.
Geometric Proof
First, we draw a triangle with side lengths  and
and  as shown in Figure 1. Next, create 4 triangles identical to it and using the triangles form a square with side lengths
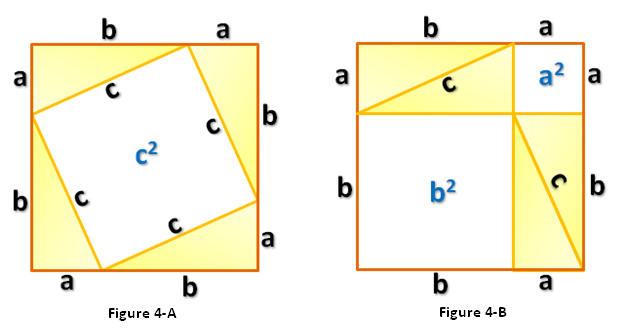
as shown in Figure 1. Next, create 4 triangles identical to it and using the triangles form a square with side lengths 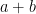 as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is
as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is 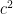 .
.
Rearranging the triangles, we can also form another square with the same side length as shown in Figure 4-B.This means that the area of the white square in the Figure 4-A is equal to the sum of the areas of the white squares in Figure 4-B (Why?). That is, 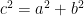 which is exactly what we want to show. *And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary
which is exactly what we want to show. *And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary  and
and 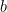 as side lengths of a right triangle), this implies that the equation
as side lengths of a right triangle), this implies that the equation 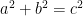 stated above is always true.
stated above is always true.
Exercise 5: Prove that the quadrilateral with side length C in Figure 4-A is a square.
Algebraic Proof
Method 1: 
Method 2: 
Methods 1 and 2 calculated the area of the same square, therefore they must be equal. This means that we can equate both expressions. Equating we have,
which is exactly what we want to show.
Subscribe to:
Posts (Atom)





 2:03 AM
2:03 AM
 Muhammad Yusuf
, Posted in
Muhammad Yusuf
, Posted in