For the 100th time (kidding), recall that the Pythagorean Theorem states that in a right triangle with side lengths  and , where  is the hypotenuse, the equation 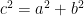  is satisfied. For example, if we have a triangle with side lengths  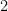and 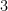 units, then the hypotenuse is 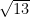. The converse of the Pythagorean theorem is also true: If you have side lengths,  and , which satisfies the equation above, we are sure that the angle opposite to the longest side is a right angle.

We are familiar with right triangles with integral sides. The triangle with sides 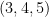 units, for instance, is a right triangle.  This is also the same with  and 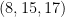.  We will call this triples, the Pythagorean triples ,or geometrically, right triangles having integral side lengths.

The first thing that we can observe about the Pythagorean triples is that there are infinitely many of them. The triple 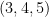, for example, can be multiplied by any positive integer to produce another Pythagorean triple. For example  is also a Pythagorean triple.  The proof is intuitively discussed below.

Theorem: There are infinitely many Pythagorean Triples.

Proof: We have discussed that two triangles that are similar are of the same shape, but not necessarily of the same size. We also know that similar triangles have congruent corresponding angles.  Therefore, if a triangle with integral side lengths  is right, multiplying the side lengths with any positive integer 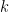 changes only the size and not the shape.   Therefore, our new triangle with side lengths  is also right.

Since there are infinitely many positive integers which we can substitute to 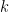, we can therefore conclude that there are infinitely many Pythagorean Triples.